Difference between revisions of "Triangulation"
From Yade
| Line 1: | Line 1: | ||
| ⚫ | |||
| ⚫ | |||
| ⚫ | TesselationWrapper (still in development) can be used for building and performing basic operations on the triangulation or tesselation of sphere packings. It should be accessed directly from python or included in another engine doing more complex things (e.g. MicroMacroAnalyser - see below, TriangulationCollider, VolumicContactLaw). |
||
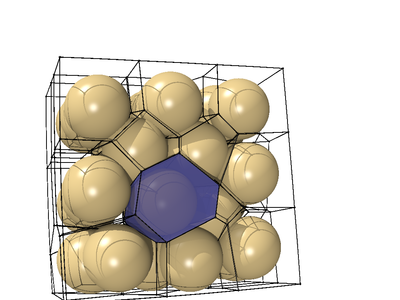
| + | [[File:cell_volume.png|400px|thumb|right|Fig.2 Defining a local volume for spheres in a packing ([[Publications | Hartong et al. (2010)]])]] |
||
| ⚫ | |||
| − | [[File:StrainLocPeriodic.png]] |
||
| + | |||
| ⚫ | |||
| ⚫ | TesselationWrapper (still in development) can be used for building and performing basic operations on the triangulation or tesselation of sphere packings. It should be accessed directly from python or included in another engine doing more complex things (e.g. MicroMacroAnalyser - see below, TriangulationCollider, VolumicContactLaw). |
||
===Main members :=== |
===Main members :=== |
||
Revision as of 18:00, 22 June 2010

TesselationWrapper
TesselationWrapper (still in development) can be used for building and performing basic operations on the triangulation or tesselation of sphere packings. It should be accessed directly from python or included in another engine doing more complex things (e.g. MicroMacroAnalyser - see below, TriangulationCollider, VolumicContactLaw).
Main members :
<source lang="cpp"> ///Insert a sphere, "id" will be used by some getters to retrieve spheres. insert (double x, double y, double z, double rad, unsigned int id)
///A faster version of insert. bool insertSceneSpheres (const Scene *scene)
///Move one sphere to the new position (x,y,z) and maintain triangulation (invalidates the tesselation). bool move (double x, double y, double z, double rad, unsigned int id)
///Reset the triangulation. void clear (void)
///Add axis aligned bounding planes (modelised as spheres with (almost) infinite radius). void AddBoundingPlanes (void)
///Force boudaries at positions not equal to precomputed ones. void AddBoundingPlanes (double pminx, double pmaxx, double pminy, double pmaxy, double pminz, double pmaxz, double dt)
///Compute voronoi centers then stop (don't compute anything else). void ComputeTesselation (void)
///Compute volume of each Voronoi cell void ComputeVolumes (void)
///Get volume of the sphere inserted with indentifier "id"". double Volume (unsigned int id)
///number of facets in the tesselation (finite branches of the triangulation) unsigned int NumberOfFacets (bool initIters = false)
///set first and last facets, set facet_it = facet_begin void InitIter (void)
///set facet = next pair (body1->id,body2->id), returns facet_it==facet_end bool nextFacet (std::pair< unsigned int, unsigned int > &facet) </source>
MicroMacroAnalyzer
The engine MicroMacroAnalyzer computes quantities like fabric tensor, local porosity, local deformation, and other micromechanicaly defined quantities based on triangulation/tesselation of the packing.
Discussion
Currently, if you put MicroMacro engine in your simulation, MMA::action() will (in short) : - scan bodies and build a regular(*) triangulation of the spheres each N iterations; - compute the average strain in each tetrahedron and assign it to grains (so that the "strain" of one grain is a sum over adjacent tetrahedra), based on the dispacements of particules on the interval [n,n+N]. - save the state of the sample in a text file (with a specific convention), so that strains can be recomputed later (out of yade) with different interval sizes (like [n,n+2N], [n,n+3N], etc.) - write local strains, porosity, fabric tensor, and other micromechanical quantities in txt files too.
Problems : - This engine is doing always the same thing, you can't change what it does if you don't modify the code and recompile. It is a pitty, since many geometrical functions available in lib/Triangulation could be usefull as well (e.g. computing the dual Voronoi graph). - If you want to access to quantities like porosity at the scale of tetrahedra, you have no way to do that in yade, because you need to access the CGAL structure using the concepts of cell_iterators, edge_iterators,... which are not defined in yade.
So, I'm wondering how to improve that, and I hesitate between 2 approaches :
a) enrich the interface of TesselationWrapper or MicroMacro, so that instead of just "MM::action()", many members could be accessed via python, and different things can be computed on demand, and returned in a standard format. e.g. for the porosity in a cell of the triangulation, there could something like:
pair<int [4], Real porosity> MMAnalyzer::porosityInNextCell (void);// usage : while (porosity!=-1) porosity = porosityInNextCell().second;
b) expose and make full usage of all typedefs defined in def_types.h. In that case, no need for interface any more, the full lists of edges, cells, or facets can be visited, but the user need to learn how to use CGAL and/or my triangulation classes before doing anything. Example :
for (finite_cell_iterator cell=MMA->triangulation->finite_cells_begin; cell != MMA->triangulation->finite_cells_end; cell++) {
porosity = MMA::Porosity(cell);
if (cell->vertex(2)->id == x) do something;//etc.
}
(*) Regular is for weighted points (center + radius), while the usual Delaunay is for points. It can make a big difference (and Delaunay can give stupid result) when radii are not all the same.